Coloquio: El largo gracias
- 04-12-2025 14:00 |
- Aula Federman
Investigadores del Departamento de Física publicaron este trabajo luego de su experiencia en la comisión para respuesta temprana en modelado de COVID, donde brindaron conocimientos y herramientas científicas a las autoridades a través del Ministerio de Ciencia, Tecnología e Innovación de la Nación. El paper es resultado, además, de una colaboración posterior con la empresa GranData, cuyo CEO - físico y egresado del Departamento- aportó datos sobre movilidad de celulares en Argentina.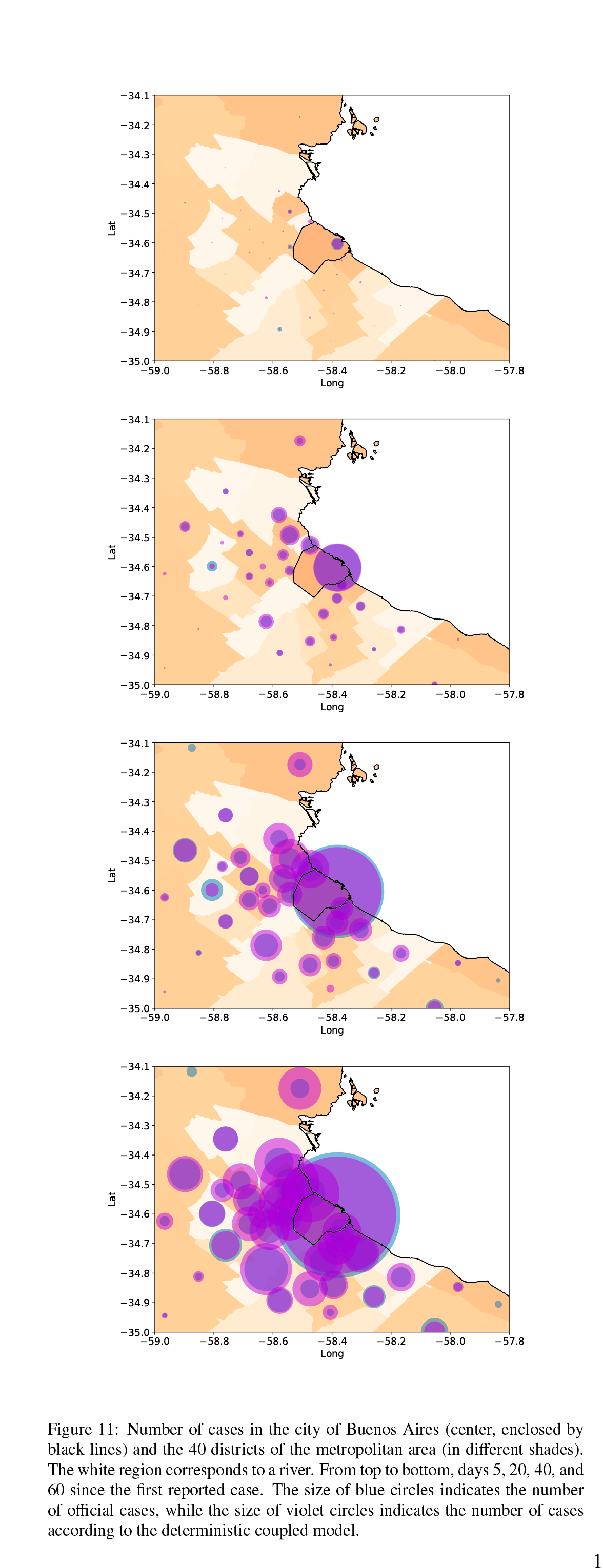
Los modelos no son oráculos infalibles, sino herramientas que transforman datos en información, por medio de distintas hipótesis, sobre la propagación del virus. Por lo tanto, la calidad de la información que pueden proporcionarnos resulta tan buena como los datos que reciben y las hipótesis que los sustentan. Hay modelos simples que nos permiten ganar un entendimiento conceptual sobre cómo un virus se propaga en una gran población de individuos, y también modelos más y más complejos que intentan generar pronósticos confiables.
En la publicación, los autores exploraron esta jerarquía de modelos -desde lo simple hacia lo complejo- en el contexto de la pandemia, esencialmente en la zona de CABA y el Gran Buenos Aires. El estudio pondera distintas lecciones sobre cómo puede y debe abordarse el modelado temprano de la epidemia; conclusiones para compartir con una comunidad científica que, al igual que el resto de la población, se enfrenta por vez primera a un desafío de esas características. Las dos lecciones más importantes que destacan los investigadores en este trabajo son, por un lado, la necesidad de ser extremadamente cuidadosos en el uso de modelos simples para evaluar efectos de políticas en salud pública. Y por otro, la ventaja que aportan los datos de movilidad provistos por teléfonos celulares para inferir tasas de contagio y vislumbrar la dinámica de la epidemia en el futuro.
La movilidad de los individuos marca el ritmo de la epidemia
La primera conclusión del trabajo es que en un país relativamente periférico como Argentina, es indispensable incorporar a los modelos datos sobre los viajeros infectados en el exterior. Los primeros casos registrados en el país no fueron el resultado de propagación local, sino de los llamados casos importados. Los autores advierten que si esta distinción no es tenida en cuenta en los modelos se sobreestima la tasa de infección y el número reproductivo básico R0, ya que se atribuye a contagio local un crecimiento que debe ser explicado por el arribo al país de individuos infectados en otros países.
Los modelos deterministas basados en compartimientos, tales como el SEIR, tratan a la población como un número continuo, de forma tal que es posible tener, por ejemplo, 0.2 individuos infectados. Y siempre que exista incluso una muy pequeña fracción de infectados, si el número reproductivo es mayor a 1, los modelos predicen una propagación casi total de la enfermedad (cerca del 80% de la población acabará infectada). Para superar estas limitaciones, el presente trabajo investiga también el uso de modelos estocásticos. Los modelos estocásticos tratan a la población como un conjunto de unidades discretas -es decir, personas- y producen pronósticos basados en la probabilidad de contagio, de forma tal que si hay pocos individuos infectados existe una probabilidad significativa de que el modelo pronostique la extinción local de la epidemia.
Los modelos como el SEIR son extremadamente sencillos - dado que no se ocupan de modelar los distintos tipos de interacciones que ocurren en un territorio y sus distribuciones geográficas-, son modelos homogéneos, asumen que los individuos pueden mezclarse indistintamente entre sí. La simplicidad de estos modelos suele requerir un ajuste de parámetros, es decir, cuando se los utiliza resulta necesario explorar rango de tasas de infección hasta encontrar aquella que mejor reproduce la curva de casos conocidos. Una vez que se encuentra esa tasa de infección se generan curvas con números de casos acumulados, las cuales se aproximan considerablemente a los datos oficiales. Pero eso no es sorprendente, precisamente porque se elige la tasa de infección para que ocurra. La pregunta central es si la tasa de infección inferida también será útil para el pronóstico de casos futuros, los cuales no fueron tenidos en cuenta durante el ajuste.
Otra de las lecciones importantes reportadas por los investigadores concierne al uso de modelos estocásticos que no incorporen información empírica confiable sobre la población: si para superar las incertezas se producen muchas reproducciones independientes de un modelo estocástico y luego se obtiene el promedio, el resultado converge al predicho por la versión determinista del modelo. Es necesario, entonces, incrementar el realismo de los modelos, y para eso es necesario inyectar más datos a los mismos.
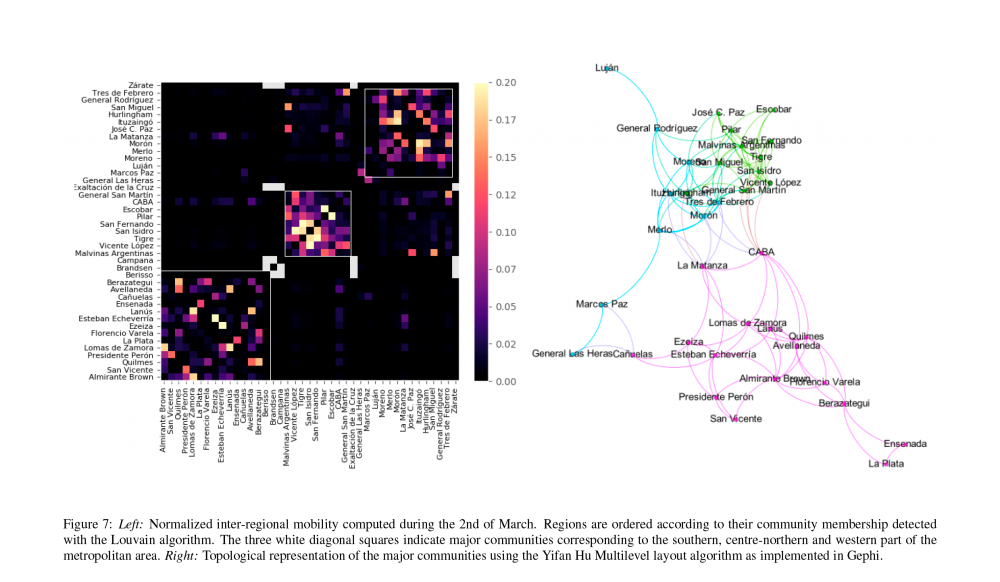
Con ese objetivo, los investigadores recurrieron a datos de movilidad basados en telefonía celular, proporcionados por la empresa GranData. De este modo es posible estimar la circulación local en cada distrito del Gran Buenos Aires y CABA, así como el tránsito entre ellos. Los investigadores observaron una caída abrupta de ambos estimativos de movilidad desde el día 19 de marzo (el comienzo de la cuarentena); luego, combinaron estos datos para construir modelos no-homogéneos y así pudieron modular la tasa de infección en base a la movilidad local. Como resultado de estos esfuerzos, obtuvieron modelos estocásticos y deterministas capaces de reproducir acertadamente la evolución de la pandemia, pero sin necesidad de realizar ajuste de parámetros. Además, verificaron que la estructura de la red de tráfico inferida de telefonía celular es fundamental para la precisión de los modelos. Utilizar una red diferente (por ejemplo, un versión permutada al azar de la red original) reduce la precisión de los modelos. Por lo tanto, es de suponer que obtener una versión mejorada de la red de tráfico resultará en modelos aún más precisos.
En conclusión, el modelado de la epidemia no puede prescindir de datos de movilidad, y éstos deben ser lo más realistas y exhaustivos posible. Así, este trabajo mostró que para el caso de una megaciudad como Buenos Aires y sus región metropolitana existe una relación directa entre movilidad y tasa de contagio, y que la información de movilidad provista por teléfonos celulares es muy útil para inferir escenarios futuros de la epidemia. Por otro lado, es recomendable ser extremadamente cuidadosos al utilizar modelos sencillos para evaluar políticas de salud pública, porque las potenciales consecuencias de esas decisiones son demasiado importantes como para sustentarlas con aproximaciones poco realistas.
Aislamientos intermitentes
Se estima que el número reproductivo R0 en Argentina se mantuvo en un valor cercano a 1 como resultado del aislamiento que comenzó el 19 de marzo. Los investigadores del trabajo mostraron que en una una pandemia como la actual, el R0 obtenido de implementar una cuarentena periódica será cercano al promedio entre el R0 durante los días de aislamiento extremo y durante los días con mayor contacto social, según la fase de cuarentena que experimenten. Y, para que la pandemia se encuentre controlada, ese número deberá ser menor a uno.
A esta limitación se suma otra: en los días de trabajo y actividad normal, el número de infectados crece y por lo tanto aumenta el tamaño de los focos. Así, retroceder en la fase de la cuarentena, aun luego de esperar varios días, no significa regresar al estado previo: el número de personas susceptibles de ser contagiadas crece con cada repetición, llevando al sistema a escenarios que los modelos homogéneos no pueden capturar. ¿Cuán intenso debe ser el distanciamiento para que el promedio sea menor a 1? ¿Es realista esperar que esos niveles de aislamiento logren obtenerse, dado que el esfuerzo continuo de toda la nación apenas alcanzó para llevar el R0 a valores ligeramente inferiores a 1? Estas son algunas de las preguntas que se plantean en el trabajo, cuya respuestas buscan ser críticas; entender el efecto de ciertas medidas de contención; y evitar decisiones desacertadas en política sanitaria.
Todos los modelos epidemiológicos fallan eventualmente. Ganar confianza en la predicción de los modelos requiere de trabajo constante para la recopilación e incorporación continua de datos actualizados - no solo del número oficial de casos, sino sobre los patrones de movilidad en las regiones donde se desea producir un pronóstico. Y si usamos modelos para proponer políticas de contención, el estándar con el que juzgamos a dichos modelos debería ser altísimo. Es fundamental incorporar la lección de aproximarse a los modelos con una actitud escéptica, cuestionando sus hipótesis y mecanismos, pero al mismo tiempo con esperanza en la posibilidad de una mejora continua, únicamente limitada por la precisión y validez de los datos que sumamos a nuestros modelos.
Lessons from being challenged by COVID-19Chaos, Solitons and Fractals: the interdisciplinary journal of Nonlinear Science, and Nonequilibrium and Complex Phenomena E. Tagliazucchi1, P. Balenzuela1, M. Travizano2, G.B. Mindlin1, P.D. Mininni1 1 Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Física, & IFIBA, CONICET, Ciudad Universitaria, Buenos Aires, Argentina. 2 Grandata Labs, 550 15th Street, San Francisco, 94103, California, USA. Publicado: 23 de mayo de 2020 |
Conceptos relevantes
Tasa de contagio, de contacto efectivo, o de infección: Una medida del número de contactos promedio que ocurren por día entre individuos infectados e individuos susceptibles, y que terminan en un contagio. Da una idea de la “velocidad” a la cual la infección se transmite.
R0: una cantidad útil para entender si la epidemia está avanzando, retrocediendo, o si se mantiene estable (R0 mayor, menor, y cercano a 1, respectivamente).
Modelo determinista: un modelo en el que las mismas condiciones de inicio produce siempre la misma evolución del sistema, sin que el azar pueda jugar ningún rol. En epidemiología matemática, este tipo de modelos suele estar descrito por ecuaciones diferenciales.
SEIR: un modelo epidemiológico sencillo que divide a la población en cuatro compartimentos: los individuos Susceptibles, los Expuestos, los Infecciosos, y los Recuperados. Este tipo de modelos permite considerar infecciones que tienen un tiempo de incubación.
Modelo estocástico: un modelo en el que las cantidades, aunque tengan reglas prescritas, pueden fluctuar al azar. Este tipo de modelos permite contemplar casos en los que nadie se contagia y una epidemia se extingue rápidamente, o en el que el número de contagios por obra del azar es muy alto.
Modelos homogéneos : En un modelo homogéneo, el contacto de una persona infecciosa puede ocurrir con cualquier otra persona en la población, independientemente del lugar donde vive, su edad, o cualquier otra característica.
Modelos no-homogéneos o heterogéneos : En estos modelos el contacto entre un individuo infeccioso con otras personas no tiene la misma probabilidad de ocurrencia para todos. La tasa de contactos puede ser diferente de acuerdo a dónde viven, la edad de los individuos, etc.
Foco: una región o lugar con los factores epidemiológicos necesarios para la transmisión de una infección, como por ejemplo individuos infectados, un grupo de individuos susceptibles, y condiciones ambientes que permitan el contagio.